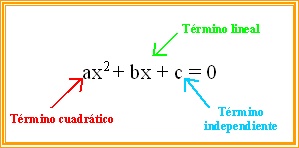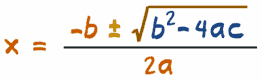Podemos definir a las matemáticas financieras como la rama de la Matemática que estudia las variaciones que se producen en los capitales financieros en el transcurso de un determinado periodo de tiempo.
Las “mates financieras” pueden ser vistas desde 2 puntos de vista, como son: las operaciones financieras simples (interés y descuento) y complejas (rentas). Se define, por tanto, operación financiera como la sustitución de uno o más capitales por otro/s equivalentes en distintos momentos de tiempo, mediante la aplicación de una determinada ley financiera.
El mundo de las matemáticas financieras es muy amplio y variado, por lo que, para quien no esté familiarizado con esta rama económica, le invito a que pueda consultar alguno de los múltiples y completos manuales sobre el tema que se pueden encontrar en la red, como el siguiente ejemplo que os propongo, por su sencillez explicativa:
MANUAL MATEMÁTICAS FINANCIERAS
En el siguiente post lo que me propongo es simplemente resolver un ejercicio, en la que quizás sea la parte más compleja de su ejecución, que no es otra que el cálculo de la rentabilidad efectiva de una operación compuesta; para lo que elegiré una operación de descuento ejemplificada mediante una letra del tesoro (concepto muy de actualidad por las emisiones de deuda pública y de la Prima de Riesgo).
Las letras del tesoro (Según la Norma de registro y valoración 8ª) son valores de renta fija a corto plazo (menos de 12 meses) representados exclusivamente por anotaciones en cuenta (no existe un documento físico en sí, como sería el caso de las acciones). Se crearon en junio de 1987, cuando se puso en funcionamiento el Mercado de Deuda Pública en Anotaciones. Las Letras se emiten mediante subasta y su importe mínimo es de 1.000 euros (siendo el resto de importes siempre múltiplos de esta cifra). Son valores emitidos al descuento, por lo que su precio de adquisición es inferior al importe que el inversor recibirá en el momento del reembolso. La diferencia entre el valor de reembolso de la Letra (1.000 euros) y su precio de adquisición será el interés o rendimiento generado por la Letra del Tesoro.
Podéis ampliar información sobre este producto financiero en el siguiente enlace:
EJEMPLO PRÁCTICO DE DESCUENTO COMPUESTO
Una vez introducidos los conceptos imprescindibles para analizar el ejemplo práctico que me propongo resolver mediante el uso de las matemáticas financieras, pasaré a ofrecer los datos del ejercicio.
- En enero del año 2013 una empresa compra una letra del tesoro por 100 € (para simplificar los datos),
- pagando de gastos 10 €.
- El interés anual es del 4 %, pagadero por años vencidos el 31 de diciembre.
- La letra tiene un vencimiento de tres años al 110 % del nominal.
¿En este caso cuál sería el tipo de descuento efectivo o real de la operación? Al tratarse de una operación compuesta, sabemos a ciencia cierta que no puede coincidir con el del tipo de interés del 4%, ya que se actualizan los intereses año a año, además de que se deben incluir los gastos, por lo que debemos saber cuál es la “traducción de ese 4% en interés efectivo e la operación de descuento (d)”
Así que a continuación resolveré la operación matemáticamente:
Al final de la operación recibiremos 100€+(100*0.04), o sea el capital inicial más los intereses del 4%, que suman 104€, pero recibiremos un interés al final del primer año equivalente al 4% del capital inicial, o sea de 4€, que debemos actualizar; al final del 2º año se nos pagará el valor de la letra más los correspondientes intereses,más los gastos de la operación junto con los intereses de ese año (100+4+10=114). Al tratarse de una operación de descuento la capitalización es inversa, es decir debemos actualizar los intereses futuros al momento inicial (“exponentes negativos”).
Con lo que la operación se resolvería así:
- 104=4*(1+d)-¹+114*(1+d)-² –> d?? (el tipo de descuento es lo que nos proponemos obtener)
Como no es operativo trabajar con exponentes negativos, los pasamos a positivos pasándolos todos ellos al denominador:
- 104=4/(1+d)¹+114/(1+d)²; ahora deberemos multiplicar todos los numeradores por el denominador de mayor valor ((1+d)²) para poder despejar:
- 104*(1+d)²=4*(1+d)+114; empezamos a calcular recordando que (1+d)² es igual a 1+d²+2d² (el cuadrado del 1º, más el cuadrado del 2º, más el doble del 1º por el 2º)
Si resolvemos las cuentas tenemos que: 104+104*d²+104*2*d=4+4d+114; ahora debemos llevar todo al mismo lado de la igualdad para poder igualar a cero, obteniendo de esta forma la siguiente función cuadrática:
104*d²+204*d-14=0
Es en este punto donde surgen las principales dudas de cálculo para poder continuar, para lo cual debemos referimos a la fórmula para la resolución de la función cuadrática, y es la siguiente:
A partir de aquí ya sabemos como seguir resolviendo el problema:
Y con esto ya podemos saber que la rentabilidad final de la operación que hemos propuesto a modo de ejemplo sería del 6.63%.
Si se siguen estos sencillos pasos podremos resolver cualquier ejercicio de capitalización o de descuento sin problema alguno.
Espero que os haya resultado de utilidad.
